Data Structure That Power Your Database

最简单的数据库是什么样子的?

#!/bin/bash 
db_set () {     
 echo "$1,$2" >> database 
} 

db_get () {     
 grep "^$1," database | sed -e "s/^$1,//" | tail -n 1 
}

如上所示, 我们完成了一个最简单的 kv 数据库. 它的工作原理是: db_set 在文件末尾追加一个 kv 对; 如果对某一个 key 进行更新, 那么新的记录会继续追加写入文件, 而非覆盖; db_get 查询到最后(即最新)一条 key , 然后返回 value.

这个数据库的写效率极高 [ $O(1)$ ], 因为它单纯的就是向文件的末尾进行 append 操作. 但是代价是它的读效率非常低 [ $O(n)$ ].

为了解决读效率低的问题, 可以使用 索引 , 索引本质上是一个依附于主体数据的额外的数据结构. 它可以作为一个整体地被添加或者删除. 但是索引又会引发一个新的问题, 索引的变化依托于 写(write) 操作, 这意味着每次写都需要额外的一部分性能来更新这个数据结构, 如果数据结构过于复杂, 则会拖慢影响写的效率.

本节主要就是围绕这些索引结构及其演进来展开.

  • Hash Index
  • SSTable
  • …

Hash Index

Hash Index 的核心是维护一个 hash map, 这个数据结构广泛地存在于各个语言之中, 所以不在对其原理做过多的赘述.

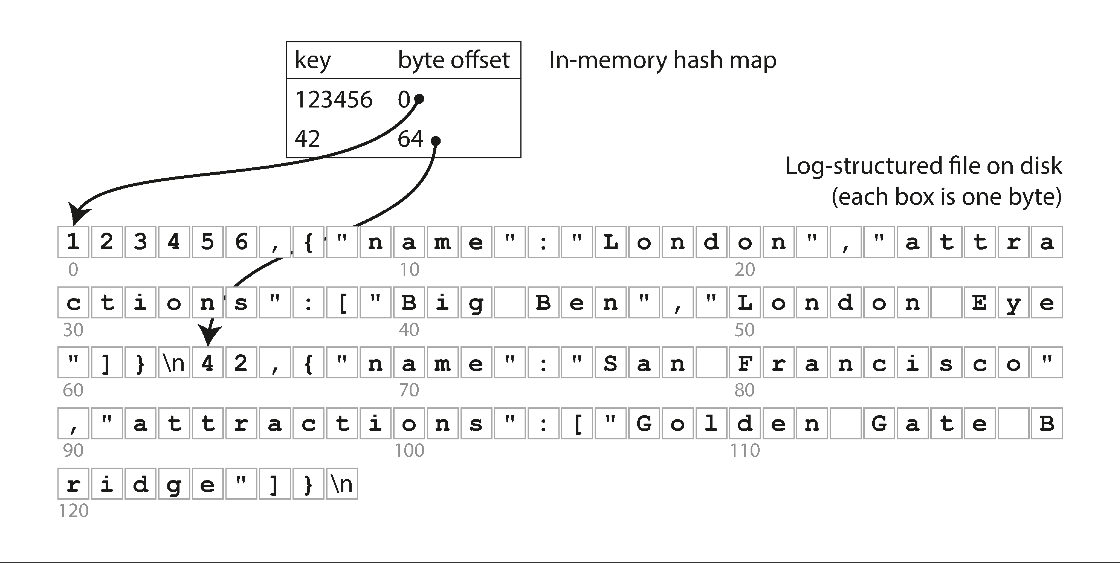
Storing a log of key-value pairs in a CSV-like format, indexed with an inmemory hash map.

Storing a log of key-value pairs in a CSV-like format, indexed with an inmemory hash map.

Hash map 为了保证查询效率, 一般是整个放在内存中.

硬盘中的 log 与内存中的 hash index 组合起来, 就能够提供较高的读写性能 (仅当内存容量 > hash map 大小时).

  • 写: 依然是文件追加写.
  • 读: 一次内存查询, 一次磁盘 seek; 如果数据已经被缓存, 则 seek 也可以省掉.

Compaction

上文所述的这种通过 append 进行写操作的数据库, 这种结构一般称之为 log-structure. log-structure 类型的数据库面临的问题主要有二, 除了上文所述的 低效读, 另一个问题是, 每一次写操作都会计入 log 文件, 这样很容易让 log 文件过大. 尤其是对于 key 的数量较少且更新频繁的数据, 新数据会导致旧数据失去价值, 从而产生大量的空间浪费. 所以需要一套压缩(Compaction)方案来保证空间使用率.

压缩的一个解决方案是将 log 文件按照一定的大小分段 (Segment), 当写满一个 segment 之后, 就将该 segment 分离出来进行压缩, 即, 丢弃该 segment 中重复的键, 相同的键仅保留最近一次写入的结果.

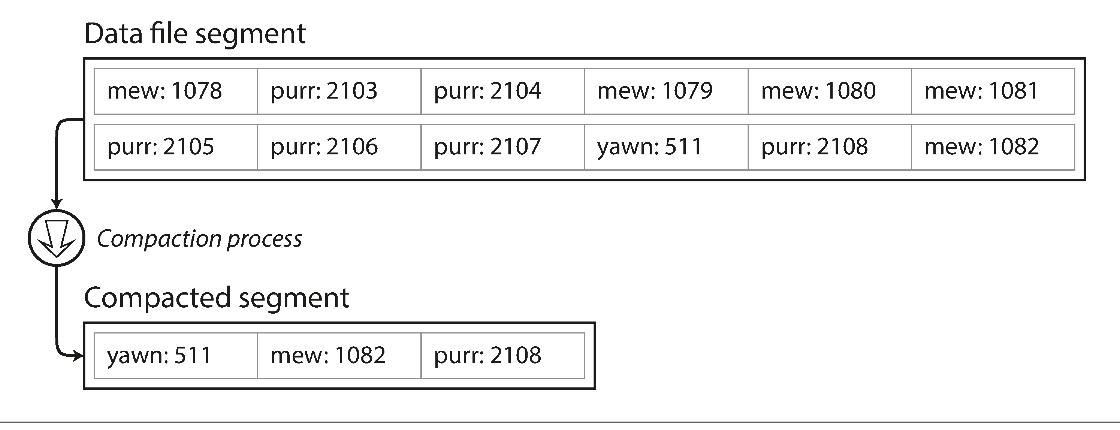
Compaction of a key-value update log (counting the number of times each cat video was played), retaining only the most recent value for each key

Compaction of a key-value update log (counting the number of times each cat video was played), retaining only the most recent value for each key

压缩之后, 旧的 segment 逻辑上占用的空间会大于或等于实际占用的空间, 所以对于这部分的 segment 可以进行合并(merge), 然后重复进行上述的压缩操作. 需要注意都是, 合并操作是在一个新的 segment 中进行的, 压缩之后, 虽然 segment 在实际上出现了空余空间, 但是在逻辑上已经锁定了(只读). 在完成合并之后, 旧的 segment 将会被删除.

每个 segment 都有自己的 Hash Index, 在进行查询时, 会按照时间顺序来进行查询任务.

log-structure 的数据库乍一看是十分简陋的, 即使有后面的压缩操作, 但依然会浪费很大的一部分空间. 但是对于原地更新型的数据库, 它具有如下的优点与不足:

  • Advantages
    1. append 操作的效率要高于 update. 因为省略了查询定位的操作. 此外, segment 的大小是固定的, 所以 update 造成的数据块大小的变化很可能会引起 segment 的重建, 造成不必要的开销. 另外, 对于 HDD 来说.
    2. 程序崩溃出错之后能够很快地进行恢复.
    3. 合并操作能够一定程度上避免碎片数据的产生.
  • Disadvantages
    1. Hash index 必须存在于内存中, 如果数据量过大, 很容易内存溢出. (如果将 Hash index 维护于硬盘中, 则会降低索引的性能)
    2. 由于 key 是无序的, 所以对于范围性的查询不友好. ( e.g: 0 < key < 100 )

SSTables and LSM-Trees

在之前的优化中, 每一个 segment 都是一个顺序的 kv 对, 它们的顺序只与被 append 的时间相关, 而 kv 本身的顺序无关紧要. 甚至乍一看, 排序操作会丧失顺序写带来的性能优势.

以 key 为排序基准的结构, 一般被称为 SST (Sorted String Table) . 这种格式有如下的好处:

  • 合并 segment 变得更为高校, 即使文件比可用内存更大. (参考合并排序算法, 多个 segment 同时进行合并)
  • 不再需要将全部的 key 维护在内存中. 可以采用 offset 的思路对 key 进行压缩. (0,1,2,3,…. ⇒ 0, 10, 20, ….)
  • 由于读取请求无论如何都需要扫描所请求范围内的多个键值对，因此可以将这些记录分组到块中，并在将其写入硬盘之前对其进行压缩 (类似json的格式化?)

构建与维护 SSTables

SSTables 在数据结构上更加接进 “树(Tree)”. 但是目前这棵树依然是仅存在于内存中的.

维护这个数据结构包含以下的几个工作:

  • 插入数据时, 保证树结构的平衡(balance), 参考红黑树. 这棵接收数据的树是维护于内存中的(memtable).
  • 当 SSTable 的容量超过阈值时, 将其转移到硬盘中. 此时这个 SSTable 成为 most recent segment. 在这个转移过程中, 可以开辟一个新的内存空间来维护新的 SSTable.
  • 当读(read)请求进入时, 先查询内存中的 memtable, 然后是 most recent segment, 以此类推, 直到命中, 返回*.*
  • 硬盘中的 segments 在不停地进行合并压缩操作.

当程序发生意外时, 硬盘中的数据不会受损, 但是内存中维护的 mamtable 会丢失, 为了避免这一情况, 最好是对 memtable 留存一份的 append log, 当数据写入硬盘时, 删除对应的 log.

LSM-Trees (Log-Structured Merge-Tree)  consists of some memory components and some disk components. Basically SSTable is just a one implemention of disk component for LSM-tree.

性能优化

  • 对于不存在的 key, 在查询时会遍历完整个 SSTable, 所以可以使用布隆过滤器(Bloom filters)来降低这种查询带来的损耗.
  • 优化压缩策略: size-tiered \ leveled compaction. (压缩策略的优化实际上是”什么情况下压缩哪些内容”的细化, 这里不作深入)

B-Tree

从结构上看, B-trees 与 SSTables 相类, 都是维护了一个以 key 排序的键值对, 以高效地进行查询的操作, 但是二者的设计逻辑是大相径庭的.

如前文所述, log-structured indexes 将数据库分为大小不一的 segments (通常是 MB 或者更大), 并且按序写入硬盘. 与之相反的是, B-trees 将数据库分为大小固定的 blocks 或者 pages (通常是 4KB, 有时会更大), 并且每次读写以页为单位. 由于硬盘也是按照固定大小进行分配的, 所以这种设计更加贴合底层硬件. (有关 page 和 block 的问题可以看这个回答)

每个 page 都有自己的 id , 用来进行逻辑上的引用, 其引用结构如下图所示.

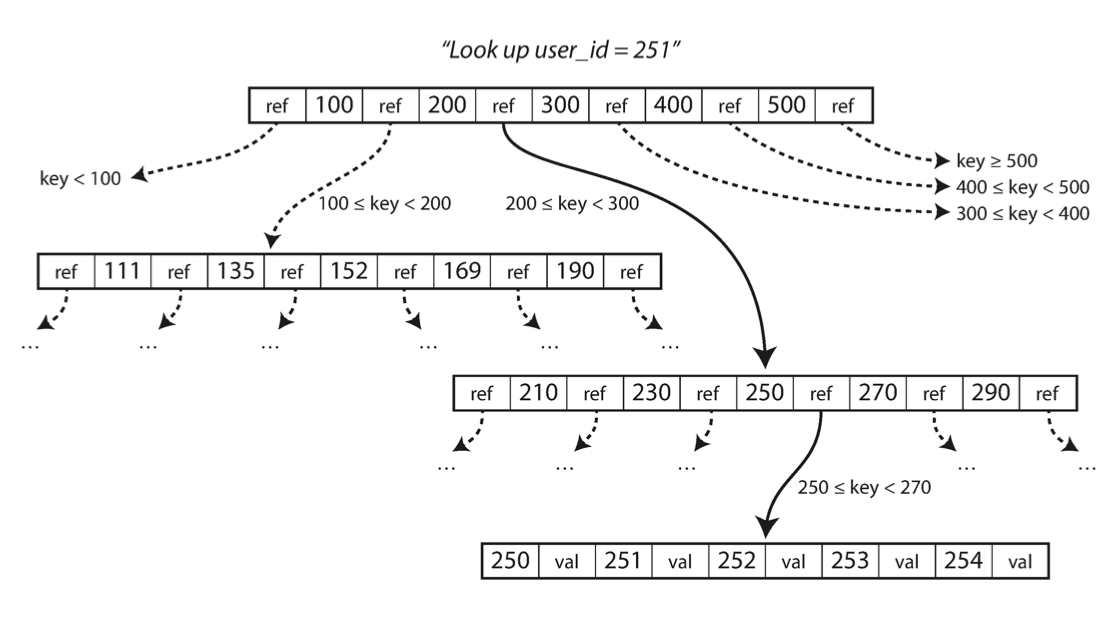
Looking up a key using a B-tree index.

Looking up a key using a B-tree index.

每个 page 包含的子页面的数量被称为分支因子(branch factor), 上图中的分支因子数量即为6. 通常, 分支因子的数量为几百个.

该图展示了一个查询的实际过程. 本质上是一个二分查找, 从根节点出发, 查找对应的区间, 直到命中 叶子节点 (leaf page) .

在对索引树进行修改时, 遵循如下的算法.

在更新的时候, 数据库根据索引定位到叶子节点, 然后将对应的数据进行更新, 最后将页回写到硬盘. 而在插入新数据的时候, 会按照既定的顺序插入索引树. 当没有足够的空间来插入 key 的时候, 会将当前页对半分解为两个新页, 然后再进行更新.

这套算法保证了索引树是一个平衡树, 也就是拥有 n 个 key 的 B-tree 深度为 $O(\log n)$. 大多数数据库的 B-tree 深度为 3 or 4 层.

$StorageSize = BranchingFactor ^ {depth} * BlockSize$

让 B-Tree 更可靠

B-Tree 的写操作是直接在硬盘上以 page 为单位进行覆盖. 某些操作(如需要分裂 page 的更新)会导致数个 page 进行级联变动, 如果在变动的过程中出现了程序崩溃, 那么索引树就会在结构上产生溃烂.

为了保证B树能够具有这样的抗崩溃(anti-crash)能力, 通常会在硬盘上外置一个数据结构, write-ahead log(WAL, also known as a redo log). 顾名思义, 它会将所有的修改操作记录下来, 在程序发生中断时用来进行恢复.

另一个需要考虑的是并发控制, 树结构通常使用 latches 来确保并发安全性. log-sturcture 在这方面要简单得多, 因为所有的合并操作都是在后台中进行, 不会受到查询的干扰.

Latches vs. Locks:

  • Latches, like mutexes, are on physical memory addresses (in bufPool). Cheap to allocate and set. Locks are on externally visible data, and named in a lock table that has a lot of data structure support (hash at least by lockname and by xact). So expensive to allocated and set (10x latches).
  • Latches, like mutexes, are held “as long as needed”. Locks are held to transaction boundaries.

优化 B-tree

  • 取 WAL 代之, 使用 copy-on-write(COW) 方案. 即, 将修改页复制到另一个地址(location), 在这个新页面进行修改, 修改完毕之后, 将父页面的引用更新. 这个方案同样适用于并发控制. Q: 只保证了原始数据, 中断恢复如何进行?
  • 不直接存储完整的 key , 而是进行压缩. 特别是在 tree 的内部的页面中，key 只需要提供足够的信息来作为范围之间的边界. 压缩 key 意味着 tree 能够有更多的分支因子, 从而降低 tree 的高度(levels).
  • pages 可以存放在硬盘的任何地方, 所以在进行范围查询的时候, 这种布局设计是非常低效的. 所以有些 B-Tree 会将叶子节点有序地存储在硬盘上, 由此能够进行高效的范围查询, 但是代价是维护成本会随着 tree 的生长愈发困难.
  • 为每个叶子节点添加兄弟指针, 这样可以避免遍历时需要到父节点查找下一个 page 的情况(回溯).
  • 借鉴 log-structure 的一些特性来进行优化, 由此衍生出一些 B-tree 的变种.

对比 B-Tree 和 LSM-Tree

从经验上看, B-Trees 在读(read)方面更快, 而 LSM-trees 在写(write) 方面更快.

但是, 基准(benchmarks) 往往是不确定的，对工作负载的细节很敏感. 你需要用特定工作负载(workload)来进行测试, 以便进行有效的比较。

LSM-Trees 的优势

一个 B-tree 索引的每段数据会至少写两遍: 一遍是 WAL, 一遍是 page. 每次更改数据都会复写整个 page, 部分引擎会复写多次. Log-Structure 索引由于 Compaction 和 merging of SSTables, 同样会重写多次. 这种入库生命周期内多次写入的行为, 被称为 “write amplification”. (SSD比较特殊, 由于它的磨损机制, 所以只能进行有限次数的重写.)

在需要进行大量”写”操作的应用中, 性能瓶颈通常在数据库到对硬盘的写入速率. 所以 write amplification 越低的, 效率越高.

LSM-Trees 的写入能力更高. 原因如下:

  • 拥有更低的 write amplification (尽管这取决于存储引擎的配置和工作负载)
  • 顺序写(sequential write)的机制更加符合磁盘的设计 (B-Tree是随机写, in place)

此外, LSM-Trees 能够进行更好的压缩, 占用的空间更小. B-tree 由于分页机制, 如果 page 写不满, 从而形成碎片(fragmentation) , 造成空间浪费. LSM-Trees 则会对碎片进行整理与压缩.

在许多的 SSD 上, 固件在内部使用了一种日志结构的算法, 在底层的存储芯片上将随机的写入转化为连续的写入, 所以存储引擎的写入模式的影响不太明显. 但是 较低的 write amplification 和 较少的碎片文件 仍然是有利的.

LSM-Trees 的劣势

LSM-Tree 的压缩进程一直在后台进行读写操作, 占用了有限的系统资源, 有时这种操作会妨碍到服务的性能,尤其是在进行代价较大的压缩操作时, 甚至会阻塞正常的请求. 相比之下, B-Tree 的性能表现更加稳定.

另一个压缩会引发的问题是, 在高写入量时, 磁盘有限的写入带宽需要在初始写入(logging和刷新memtable到硬盘)和在后台运行的压缩线程之间共享. 随着数据库的增加, 压缩线程占用的资源也会更多. 如果写入吞吐量很高, 并且压缩没有仔细配置, 压缩跟不上写入速率. 在这种情况下, 磁盘上未合并段的数量不断增加, 直到磁盘空间用完, 读取速度也会减慢, 因为它们需要检查更多段文件.

B-Tree 的一个优点是每个键只存在于索引中的一个位置, 而日志结构化的存储引擎可能在不同的段中有相同键的多个副本. 这个方面使得 B-Tree 在想要提供强大的事务语义的数据库中很有吸引力: 在许多关系数据库中, 事务隔离是通过在键范围上使用锁来实现的, 在B树索引中, 这些锁可以直接连接到树.

Reference

  1. Martin Kleppmann : “Designing Data-Intensive Application”
  2. Rui Huang : “What’s the difference between page and block in operating system?”
  3. 木鸟杂记 : ”**DDIA 读书笔记（三）：B-Tree 和 LSM-Tree”**
  4. berkeley - cs262b : “Concurrency Control and Recovery for Search Trees”